The Method of Squaring

Until now, the midpoint of an area has been defined by its calculation method. Now, however, the midpoint is defined by its actual mathematical determination:

"Accordingly, the midpoint is the point that is the middle, i.e. the most central, point in relation to all other points in the area."

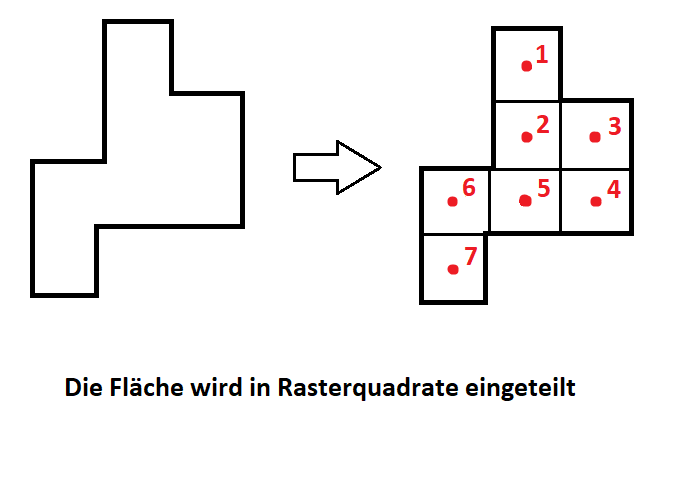
So to determine all the points in the area, it is divided into squares.

The basic idea of the squaring method is to divide the area to be calculated into squares and then identify the most central square in relation to all other squares. Accordingly, a large rectangle is drawn around the area and divided into a grid with many equally sized squares. Furthermore, all centroids of the squares that are enclosed within the area are determined. The grid squares outside the area are not considered. Then, all distances from one square centroid to every other square centroid within the area are summed up and stored for each square centroid. This results in a total distance for each square centroid, describing the distances from the centroid being calculated to every other square centroid within the area. The square centroid with the smallest total distance is output as the midpoint.

Additionally, the area of the area to be calculated can be determined from the number of filled squares and the size of a square.

In the Wikipedia article about the midpoint of Germany, the Squaring Method is mentioned under 
"Bestimmung mittels einfacher geometrischer Figuren" as method 
"Minimale Entfernungssumme nach Aufteilung der Landesfläche in (quadratische) Teilflächen".