The previous Methods in Comparison
THE METHOD OF LATITUDE AND LONGITUDE
Creating a rectangle from the outermost latitude and longitude lines of Germany's borders identifies the midpoint of Germany as being in Niederdorla.
However, this method is highly error-prone since, for a country with an irregular shape like Japan, the midpoint would end up in the sea. Consequently, this calculation method does not determine the center of the actual area but rather the center of the "stretched" rectangle.
THE METHOD OF INTERCEPTION
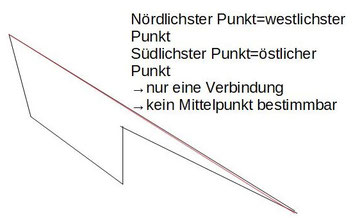
The center point of this method is calculated from the intersection of the lines connecting the northernmost and southernmost points, as well as the westernmost and easternmost points. Accordingly, the center of Germany is located in Besse near Kassel.
Just like with longitude and latitude, an irregular shape can also lead to errors. The simplest error-prone example would be an area where the northernmost point is the same as the westernmost point, and the southernmost point is the same as the easternmost point. In such a case, both connecting lines would be identical, resulting in infinitely many intersection points.
THE METHOD OF Gravity
On Wikipedia, the gravity point is referred to as a type of midpoint (center). Accordingly, it also competes for the title of "Midpoint of Germany." However, can the gravity point be the same as the midpoint of an area? Using the squaring method for calculating the midpoint, this is not the case. Therefore, the gravity point will not be further considered in the dispute over the midpoint.
The definition of the gravity point is generally known. However, the definition of the midpoint has been controversial until now. Since the squaring method has demonstrated how to describe the true midpoint of an area, the gravity point can now be compared with the center! However, this topic will be dedicated to a separate page.
THE Method of the ENCLOSING RECTANGLE
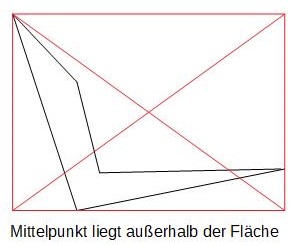
From the northernmost, southernmost, westernmost, and easternmost points, a rectangle is spanned around the area. The midpoint is determined by the intersection of the two diagonals of the rectangle.
This well-known approach is simple and intuitive but has similar inadequacies to the latitude and longitude method. Depending on how the coordinate axes are set, the spanned rectangle and thus the center rotate. This results in a center that has little chance of being accepted in the dispute over the midpoint of Germany. Even if this method can depict a reasonable midpoint, the "Japan problem" remains, where the midpoint would again end up in the sea.
THE METHOD OF MINIMUM DISTANCE TO THE STATE BORDER

This center represents the point for which the sum of the distances to evenly distributed points along the national border is the smallest. As a result, the center of Germany is located in Heiligenstadt-Flinsberg. The method pursues an interesting approach and can circumvent most of the problems of other methods. Unfortunately, the precise distribution of measurement points along the national border proves to be very challenging. A very convoluted part of the border attracts the center more strongly due to its relative length compared to a straight segment. A fitting example is a square where the right side is a straight vertical line and the left side is a highly "zigzagging" line. Ultimately, with this method, the center of the square would be significantly pulled to the left and would no longer represent the center of the area.
THE Method of the OUTER AND INNER CIRCLE
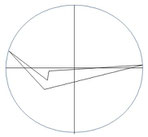
Alternatively, circles can also be used to determine the geographical center point. This method works for calculating both the midpoint and the gravity point in a triangle. Generally, however, the midpoint of the circle only reflects the center of the circle's area and neglects the remaining parts of the area to be calculated. This limitation means that while the method might provide accurate results for simple shapes like triangles, it is not suitable for more complex or irregular geographic areas, where it fails to account for all aspects of the shape.
THE ADVANTAGES OF THE SQUARING METHOD
The squaring method theoretically offers the possibility of an error-free midpoint calculation, excluding the errors and limitations of the methods previously discussed. This calculation method considers nearly 100% of the area and calculates using only this area. Issues like the "Japan problem" or distortion of the midpoint due to a "zigzag" border thus cannot occur. Furthermore, unlike the gravity point, the midpoint cannot lie outside the area, and all islands or excluded areas (holes) of the area can be successfully included. The method is applicable to any shape, no matter how complex. Only the limited computing capacity restricts the size of the squares, leading to minor inaccuracies in practice, on the order of half a kilometer.
Accordingly, we conclude that the squaring method is currently the most accurate procedure for calculating the midpoint of a geographical area. The squaring method determines the most central square in relation to all other squares of the area, thus clearly representing the "true" midpoint of the area.





